What is Mathematical Optimization and How Can it Help Your Organization?

For decades, mathematical optimization has been a must-have tool for teams dealing with complex decision problems that involve conflicting objectives, multiple constraints, and limited resources. But what is mathematical optimization, exactly? How does it compare to other types of analytics, and where does it fit in the AI spectrum? Read on to understand the key terms and use cases. 

What is mathematical optimization? 

Imagine the following business problems:  

• What is the optimal production schedule to maximize equipment utilization?  
• What is the best means of transport to deliver orders?  
• What is the optimal schedule for planning your workforce?  
• What is the optimal blend when working with natural ingredients? 

Mathematical optimization, and specifically optimization modeling, can be used to answer all of these questions. This technique is about describing a business problem in mathematical formulas or equations. It symbolically describes the decisions you need to make, the restrictions you need to uphold, and the relations between the two, to achieve a given objective. The description of such business logic is called a mathematical model. These models typically consist of: 

• variables (decisions to make), 
• constraints (the restrictions and relations that the problem is bound by),  
• and the objective (the goal you are striving for). 

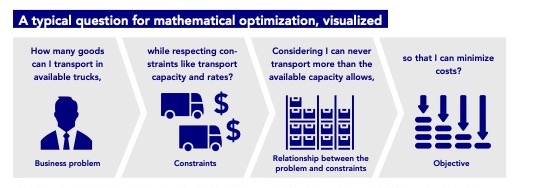
Adding data to this model and submitting it to an optimization solver, which is an algorithmic engine that solves the mathematical problem at hand, allows you to find optimal and implementable recommendations. When combined with scenario modeling, mathematical optimization allows decision-makers to analyze trade-offs and find the best course of action going forward. 

Mathematical optimization and prescriptive analytics 

Mathematical optimization is often called mathematical programming. The term is also used interchangeably with prescriptive analytics, which is a type of analytics that results in a recommended action. Mathematical optimization is often seen as “the leading prescriptive analytics tool in the market.”  

In other words, mathematical optimization is a type of prescriptive analytics. 

Unlike descriptive (focused on reporting with basic trend or pattern recognition) or predictive analytics (focused on predicting the future), prescriptive analytics determines ways in which business processes should evolve or be modified. Prescriptive analytics is crucial to make data and business rules actionable instead of only providing insight into your data’s behavior. Besides being a prescriptive analytics technology, mathematical optimization is also seen as a type of artificial intelligence (AI). 

Mathematical optimization and AI 

Gartner defines AI as “a computer engineering discipline that uses a series of mathematically or logic-based techniques that uncover and capture coding knowledge and leverage sophisticated and clever mechanisms to solve problems to interpret events, support and automate decisions, and take actions.” 

According to Gartner, there are three main categories in AI, which they classify as follows: 

• Probabilistic reasoning
• Computational logic
• Optimization techniques

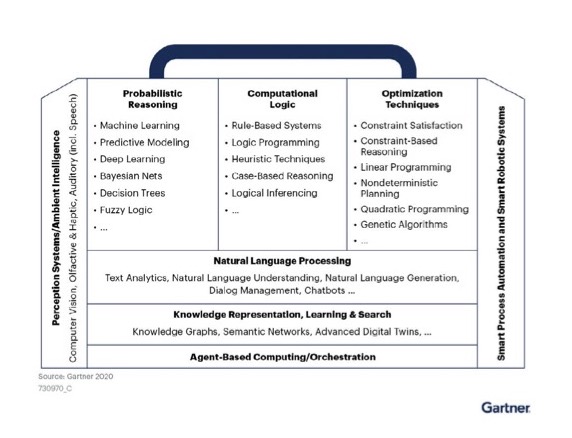
Mathematical optimization and Machine Learning (ML) 

As illustrated above, mathematical optimization and machine learning are two different AI techniques. But people often mix up the two. 

While machine learning focuses on predictions and probabilities, mathematical optimization is a prescriptive technique, focused on driving an implementable course of action. Although ML-based predictions can be used to guide certain decisions, ML is not fundamentally equipped to handle business problems that deal with many interconnected variables. This is where optimization truly excels.  

Another important distinction between machine learning and optimization is that optimization takes the business problem as the starting point, and not the data. The results of an ML algorithm are heavily dependent on available data; they often need to be tested against very large amounts of data for correctness (not just 10,000 records on a database but millions of records). Because ML models rely heavily on historical data, they can be difficult to adapt when business conditions or needs change. This makes them less flexible. ML models have trouble dealing with exceptions.  

By contrast, optimization is specifically trained to deal with exceptions as constraints are explicitly modeled. The factors that go into decision-making, and their relationships, need to be made explicit independently of the data at hand. You need knowledge of business logic. This means it might take more time upfront to develop an optimization model. But once you have a model, you can easily expand it and try out new ideas to run the business. For example, adding constraints to limit the number of suppliers, setting safety levels on inventory explicitly, forcing a minimum Co2 reduction, etc. Similarly, you can expand the number of objectives. This allows you to understand how the problem behaves under different goals (or under combined goals, so-called multi-objective optimization). 

Combining ML and Mathematical Optimization 

Clearly, the input data is still key for an optimization model to work successfully. Having good data (as complete and reliable as possible) will lead to better results. This is where machine learning can complement optimization. A widespread use case for combining both techniques is generating forecast data with a machine learning model for input into an optimization model.

Read more about combining these two AI techniques.  

Use cases for mathematical optimization 

So far, we’ve learned that optimization complements other AI techniques like machine learning. It enriches the analytics toolbox and is a highly adaptable tool. But you’re probably wondering about specific use cases. Some of the most common ones include: 

1. Supply Chain Network Design 
2. Capacity Planning 
3. Energy Market Modeling 
4. Transport Planning & Logistics Optimization 
5. Sales & Operations Planning | Integrated Business Planning 

Browse use cases for mathematical optimization by industry and application area.  

For example, in the utilities industry, grid operators like the Midcontinent Independent System Operator (MISO) in the US have used various optimization models to run real-time energy markets. These models, which were implemented over 10 years ago, delivered over $8 billion in value through 2020 and are still in use today.  

In manufacturing, models for logistics optimization can deliver over 30% in savings. Vehicle loading optimization models also help trucks drive fewer miles, which results in a lower carbon footprint. For one steel company, an AIMMS optimization model developed to optimize vehicle fill rates lowered their emissions by 550 tons per year at a single plant. This compelled them to roll out the model to other plants.  

Developing optimization models and apps 

Download our Guide to Mathematical Optimization to learn more about the tools available in the market with their pros, cons, and capabilities. You will also learn more about AIMMS Development, a toolkit for rapid optimization modeling and app development.